CMDS Math Approach
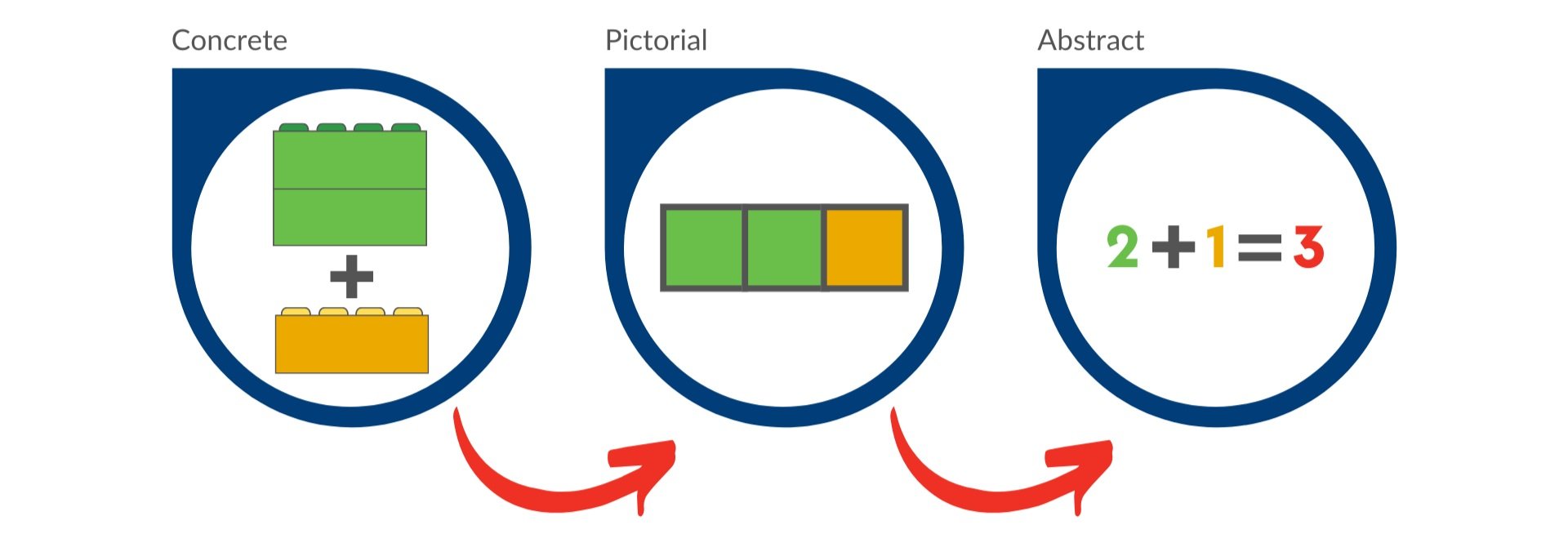
CMDS strives to develop fluent mathematical thinkers. Because mathematical concepts are abstract, we introduce topics using a “Concrete-Pictorial-Abstract” approach, which successfully constructs deep and meaningful understanding. Using concrete objects, or manipulatives, students can interact with the material in a hands-on way. Drawing or looking at pictorial models allows students to visually see the concept prior to introducing an abstract symbol. Once students have shown mastery of the concrete and pictorial stage, teachers introduce the abstract concept, or symbol.
Early Childhood
Mathematical concepts are introduced and reinforced in an age-appropriate and developmentally engaging manner. One of the foundations of play-based learning is that the teacher is active in play. She asks questions and adds knowledge and insight both in whole-class instruction and at teacher-led, small-group tables. Curiosity, math-rich vocabulary, inquiry-based activities, problem solving across curricular domains, open-ended playful explorations, music and movement are hallmarks of the math approach that CMDS has designed for our youngest learners.
Individual Practice
• Includes table-top tray activities, teacher-created games and classroom learning stations that the teacher may implement for review/extension of previously learned concepts/skills
Whole Group
• Music and movement, math vocabulary, morning meeting routines, read alouds, direct and explicit skill introduction
Teacher-Table Small-Group Instruction
• Instruction focused and differentiated by procedure, level of difficulty or work product for each student group
• Informal assessments including teacher observations, checklists and anecdotal notes are used to determine mastery.
Lower School
Teachers use a guided math workshop model to lead students through a daily mini-lesson, differentiated small-group instruction and hands-on rotations. Each piece of the math instructional lesson has a distinct and specific purpose. This enables all SK-2nd grade students to sequentially build mathematical knowledge and increase problem-solving skills.
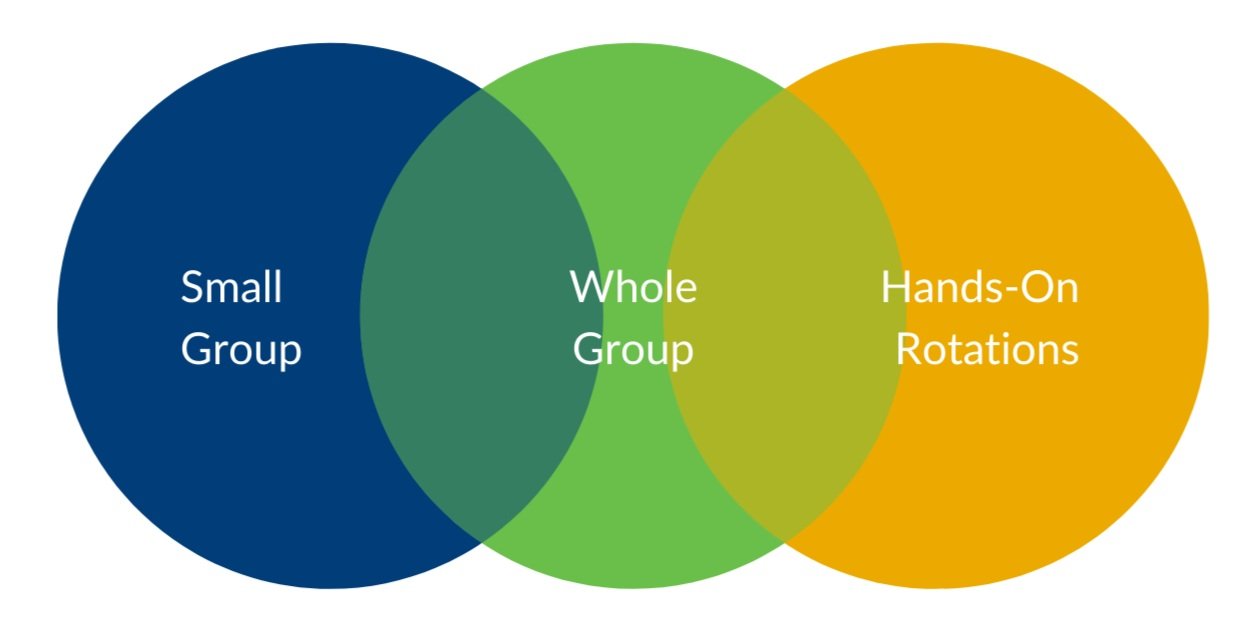
Small Group
• Instruction that can be focused and differentiated by procedure, level of difficulty or work product for each group of students
• Emphasis on conceptual understanding, procedural fluency and problem solving
• Both formal and informal assessment occur during this point of the math block, along with tests, projects and written assessments at the end of each unit.
Whole Group
• Includes mathematical discussion, active listening and an emphasis on conceptual understanding of current math skills
Hands-On Rotations
• Partner games, independent math journals, technology resources and/or individual classwork are examples that the teacher may implement for review/extension of previously learned concepts/skills.
Upper School
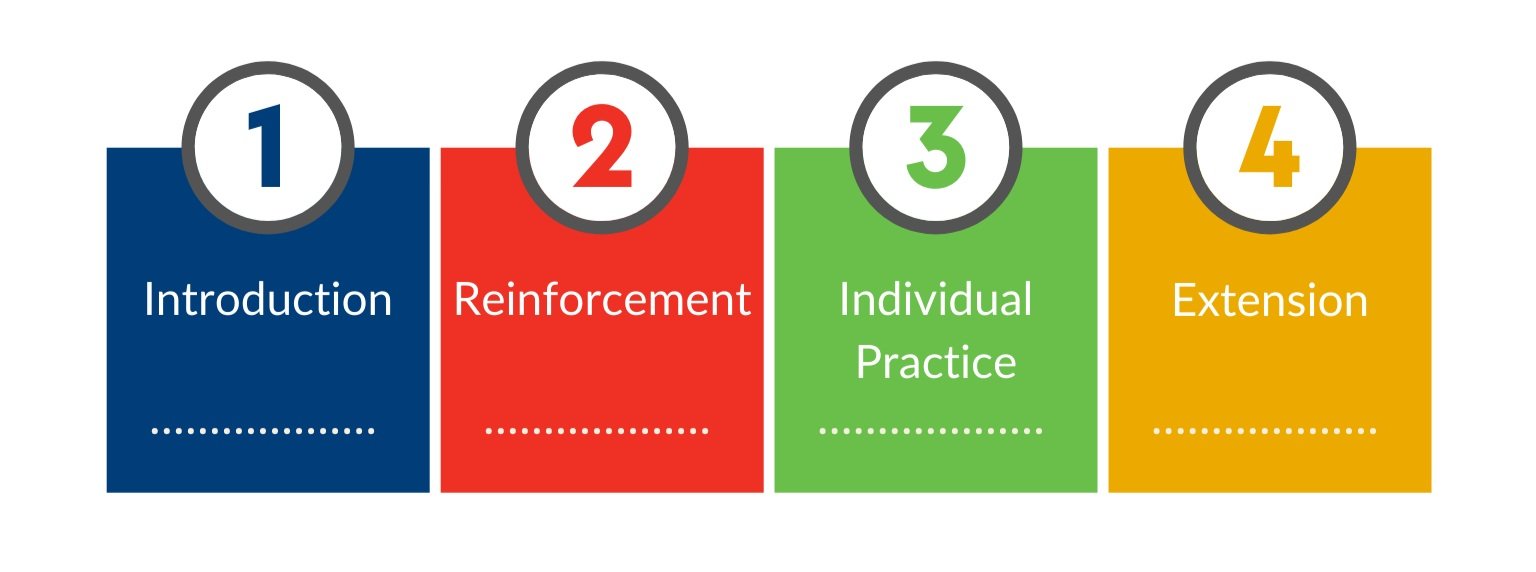
In 3rd-6th grade, each new mathematical concept or skill is taught using the following steps:
Introduction
– Contextual situation, pictorial representations and manipulatives
Reinforcement
– Activities and games are used to connect the concept/skill from introduction to the practice part of the lesson.
– Conversation and communication are used to increase math vocabulary development.Individual Practice
– Written and oral activities are used to build and increase critical thinking, problem solving and procedural fluency.
– Both formal and informal assessment occur during the math block, along with tests, projects and written assessments at the end of each unit.Extension
– The math sequence spirals and advances logically and rigorously.
– Deepens understanding of the concepts/skills
– Differentiates and challenges each student